最近在研究碰撞箱,研究到OBB,了解到其中一个判断方式就是:当图形A在图形B的全部边(线段)上的投影都与该边有交,那就说明两图形有交。而求图形A在图形B一边上的投影其实就是把图形A全部边在该边上的投影加起来,这就需要进行标题所述的判断。一开始想到从一线段两端点向另一线段作垂线,算出垂足来判断,可这属实不够优美;在群里提问后,小豆老师提出了一个更好的方法,故作此文记之。
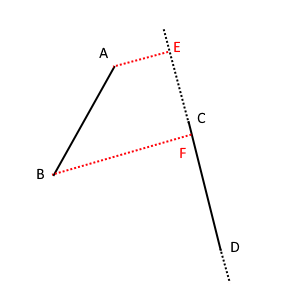
如图,AB、CD为两线段,要求AB在CD上的投影EF是否和CD有交,设坐标原点为O。
以A的投影E为例。
由于E在直线CD上,所以有\(
\vec{OE} = \vec{OC} + k_A \cdot \vec{CD} , k_A \in R \\
\)
则\(
\vec{AE} = \vec{OE} – \vec{OA}
= \vec{AC} + k_A \cdot \vec{CD}
\)
而\(
\vec{AE} \cdot \vec{CD} = 0
\)
即\(
(\vec{AC} + k_A \cdot \vec{CD}) \cdot \vec{CD} = 0 \implies
k_A = \frac{\vec{CA} \cdot {CD}}{\vec{CD}^2}
\)
同理可得\(k_B\)。
若\(k \in [0, 1]\),则说明A在直线CD上的投影E在线段CD上。
那么只要\(k_A \quad or \quad k_B \in [0, 1]\),或者一个落在\((-\infty, 0]\),另一个落在\([1, +\infty)\),AB在直线CD上的投影就和线段CD有交啦~